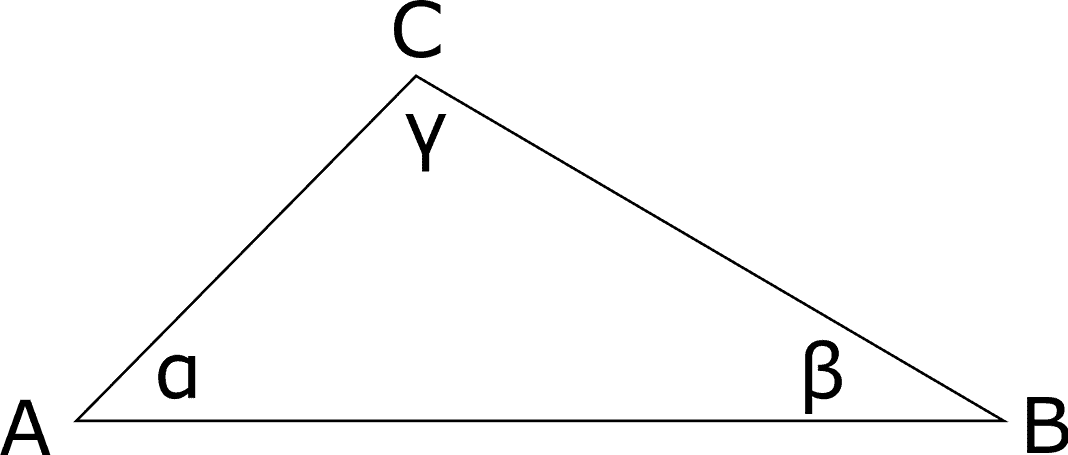
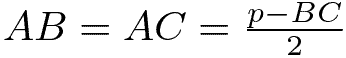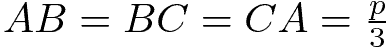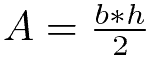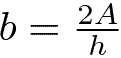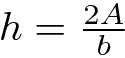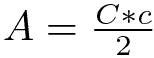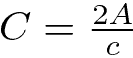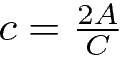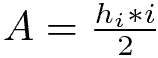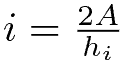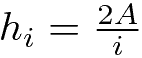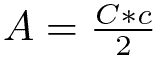Il triangolo è un poligono che ha tre lati e tre angoli. I triangoli si classificano rispetto ai lati e rispetto agli angoli.
Tipi di triangoli
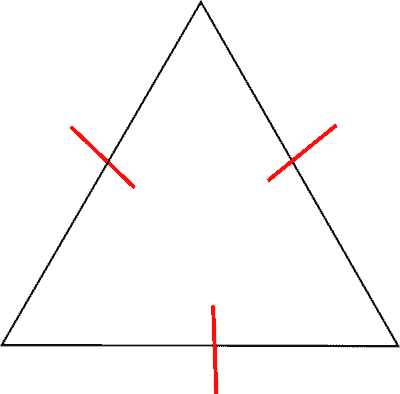
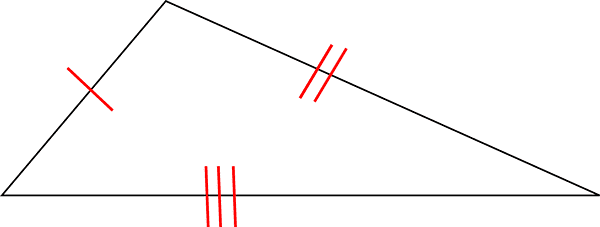
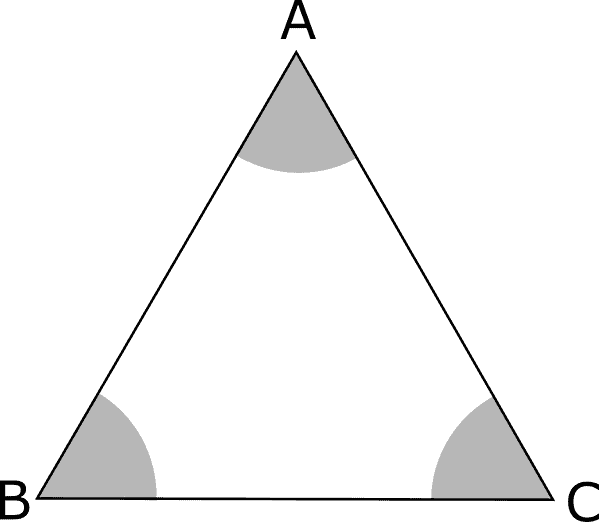
Rispetto ai lati un triangolo può essere: equilatero, isoscele e scaleno.
equilatero se ha i tre lati congruenti
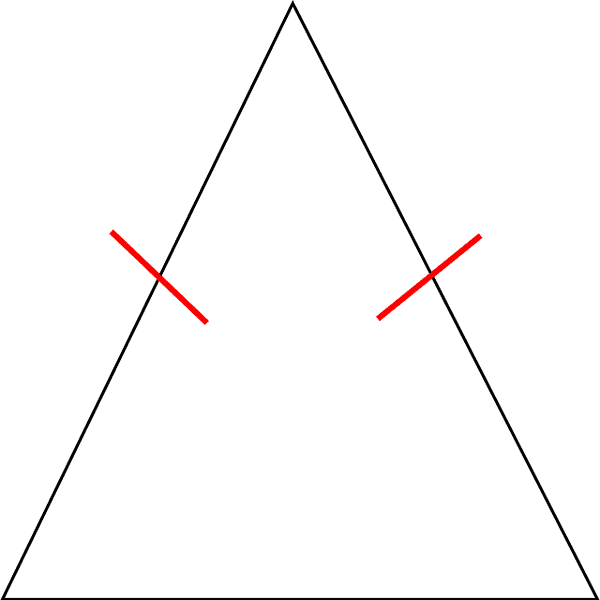
isoscele se ha due soli lati congruenti
scaleno se ha i tre lati diseguali
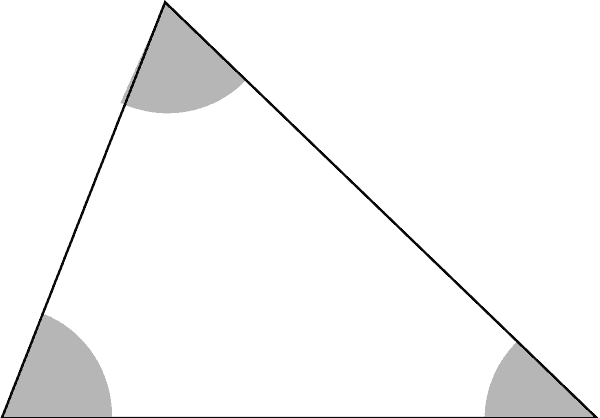
Rispetto agli angoli un triangolo può essere: acutangolo, rettangolo, ottusangolo.
acutangolo se ha tre lati acuti
rettangolo se ha un angolo retto e quindi gli altri due acuti
ottusangolo se ha un angolo ottuso e quindi gli altri due acuti.
Osservazioni sui vari tipi di triangolo
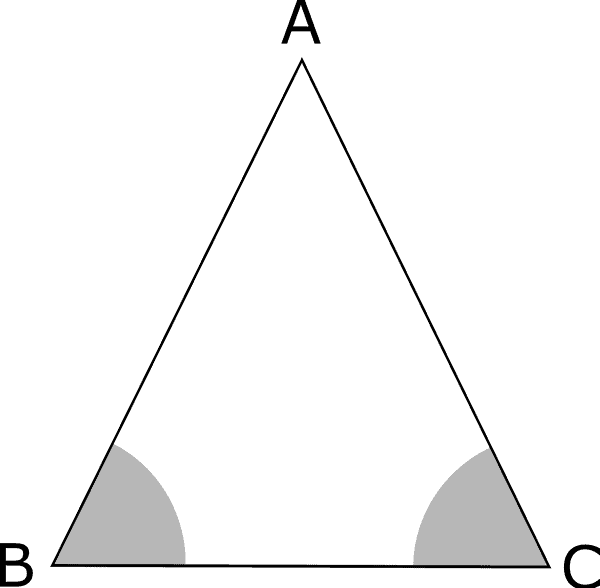
In un triangolo isoscele:
i due lati congruenti si dicono lati obliqui, il terzo lato si dice base;
l’angolo formato dai due lati congruenti si dice angolo al vertice, gli altri due angoli alla base;
i due angoli alla base sono congruenti.
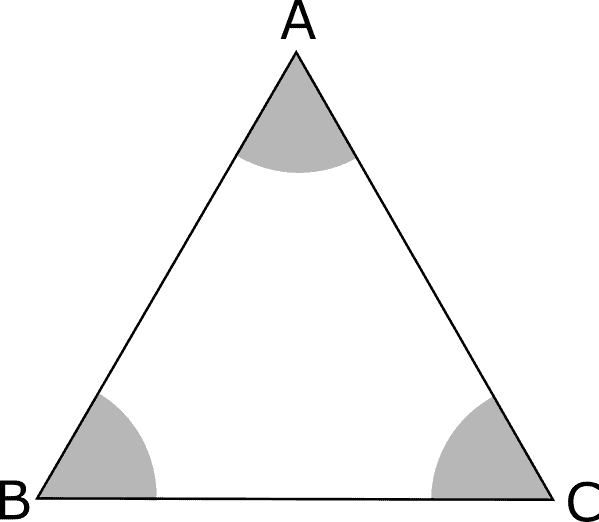
Il triangolo equilatero si può considerare isoscele rispetto ai tre lati; ne segue che gli angoli sono a due a due congruenti e quindi tutti e tre congruenti e ampi 60°.
Diciamo allora che il triangolo equilatero è anche equiangolo e quindi regolare.
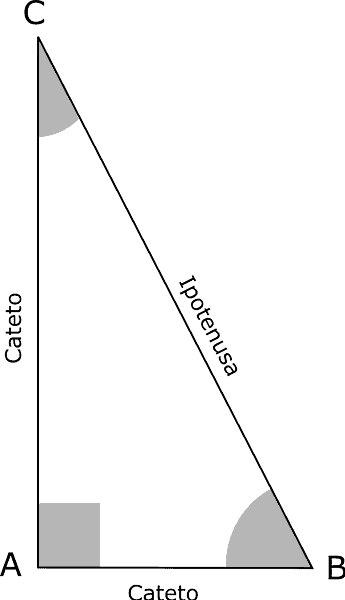
In un triangolo rettangolo invece:
i due lati che comprendono l’angolo retto si chiamano cateti;
il lato opposto all’angolo retto si chiama ipotenusa;
i due angoli acuti sono complementari, infatti si ha:
Il perimetro dei triangoli
Come per tutti i poligoni, anche per i triangoli il perimetro si ottiene sommando la misura della lunghezza dei suoi tre lati:
Formule inverse
Se conosciamo il perimetro e almeno la misura di due lati, possiamo calcolare la misura dell’altro lato:
Per il triangolo isoscele e il triangolo equilatero esistono delle formule abbreviate per il calcolo del perimetro. Eccole:
Perimetro triangolo isoscele
da cui:
Perimetro triangolo equilatero
da cui:
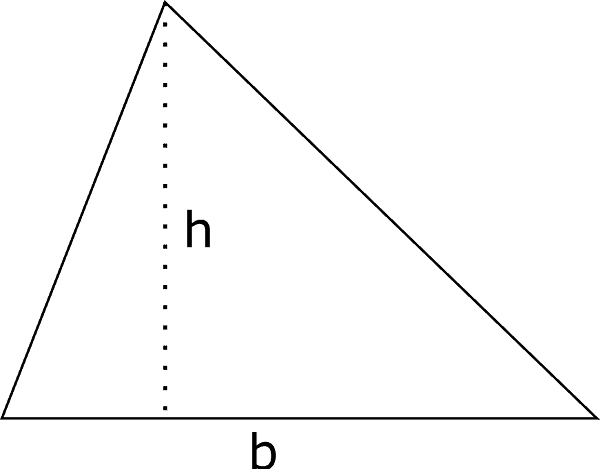
Area del triangolo
L’area del triangolo si calcola moltiplicando la misura della base per la misura dell’altezza a essa relativa e dividendo il risultato ottenuto per due.
Da cui si ricavano le formule inverse:
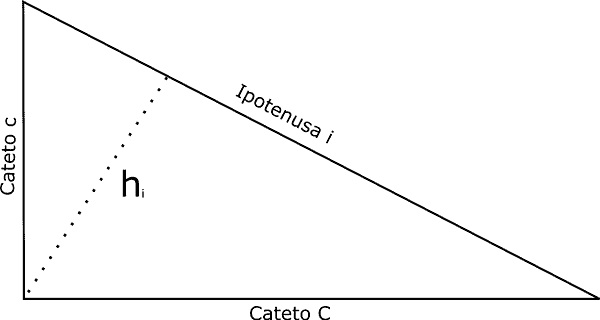
Area del triangolo rettangolo
L’area del triangolo rettangolo si calcola moltiplicando la misura dei cateti e dividendo il prodotto ottenuto per due.
da cui si ricavano le formule inverse:
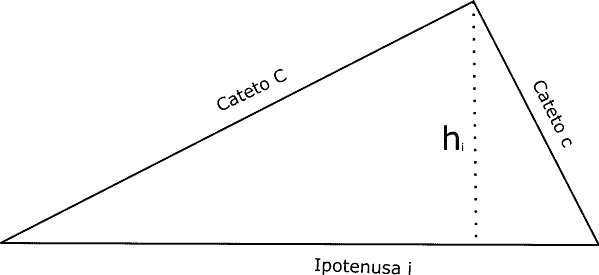
Se considero come base l’ipotenusa i, l’altezza a essa realtiva è h. Quindi:
oppure: