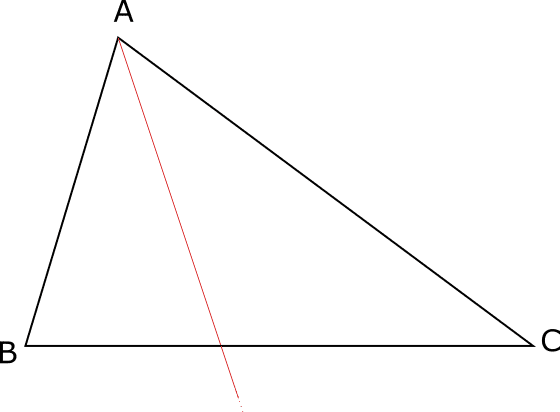
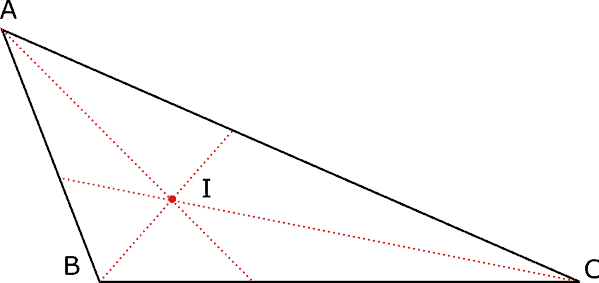
La bisettrice di un triangolo è la semiretta che taglia l’angolo di un triangolo a metà.
Consideriamo il triangolo ABC e il suo angolo di vertice A. La bisettrice dell’angolo  si dice bisettrice del triangolo di vertice A.
Quante sono le bisettrici di un triangolo?
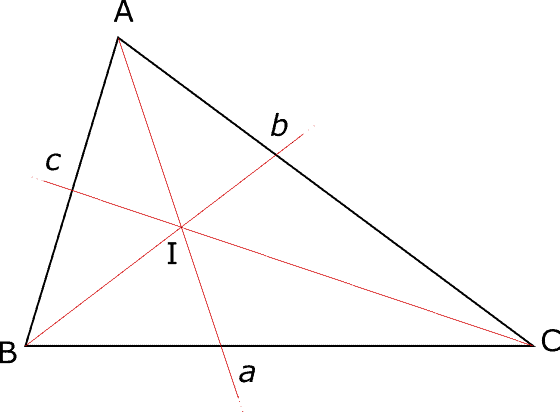
Poiché il triangolo ha tre angoli, avrà complessivamente tre bisettrici, cioè una bisettrice per ciascun angolo.
a bisettrice di vertice A;
b bisettrice di vertice B;
c bisettrice di vertice C.
Come si chiama il punto d’incontro tra le tre bisettrici?
In un qualsiasi triangolo le tre bisettrici si incontrano in un unico punto I detto incentro.
L’incentro può essere solo un punto interno al triangolo
Verifichiamo quanto appena detto.
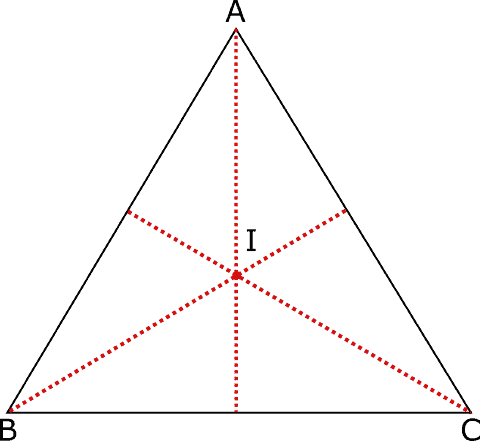
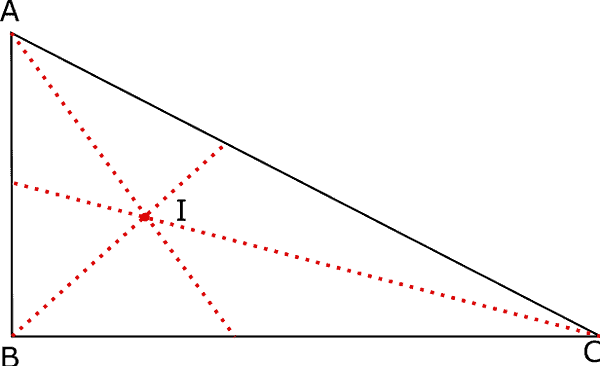
Disegniamo tre triangoli (acutangolo, rettangolo, ottusangolo) e in ciascuno di essi disegniamo le tre bisettrici e l’incentro.
Che cosa possiamo osservare?
Osserviamo che le tre bisettrici e l’incentro sono sempre interni al triangolo.
Possiamo quindi riassumere dicendo che: le tre bisettrici si incontrano in un unico punto detto incentro che è sempre interno al triangolo.
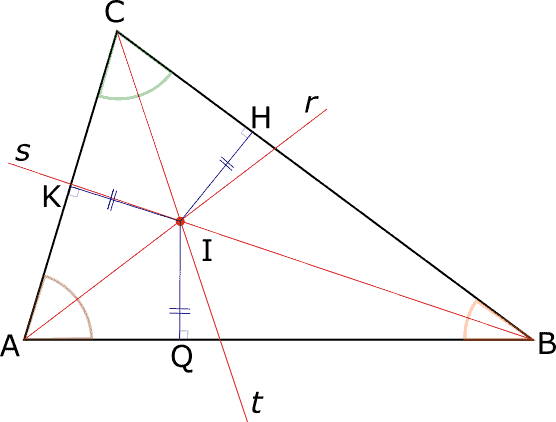
L’incentro è equidistante dai tre lati del triangolo
Verifichiamo quanto appena detto.
Disegniamo un triangolo qualsiasi, le tre bisettrici e quindi l’incentro.
Consideriamo la distanza che l’incentro ha dai tre lati AB, BC e CA, ovvero i segmenti IQ, IH, IK.
Poiché l’incentro è un punto delle tre bisettrici, i tre segmenti risultano a due a due congruenti e quindo sono tutti tra loro congruenti.
Possiamo quindi riassumere dicendo che: l’incentro di un triangolo è sempre equidistante dai tre lati del triangolo stesso.
Ti potrebbero interessare anche:
Altezza di un triangolo e ortocentro
Mediana di un triangolo e baricentro
Asse di un triangolo e circocentro
Ricorda anche che ortocentro, baricentro, incentro e circocentro sono detti punti notevoli del triangolo.