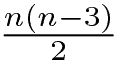I poligoni regolari in geometria sono tali se hanno tutti i lati e gli angoli congruenti. I poligoni con tutti i lati congruenti (cioè uguali) fra loro si dicono equilateri; mentre i poligoni aventi gli angoli tutti congruenti (cioè uguali) fra loro si dicono equiangoli.
Pertanto, ogni poligono che ha sia i lati che gli angoli congruenti, ossia è contemporaneamente equilatero ed equiangolo, si dice regolare.
Viceversa, un poligono che ha gli angoli e i lati fra loro disuguali si dice irregolare.
Leggi anche Poligono in geometria spiegato facile.
Nomi dei poligoni fino a 20 lati
I poligoni regolari (o irregolari) prendono nomi diversi in base al numero di lati (e quindi di angoli) del poligono stesso:
triangolo se ha 3 lati
quadrilatero se ha 4 lati
pentagono se ha 5 lati
esagono se ha 6 lati
ettagono se ha 7 lati
ottagono se ha 8 lati
e ancora:
ennagono se ha 9 lati; decagono se ha 10 lati; endecagono se ha 11 lati; dodecagono se ha 12 lati; pentadecagono se ha 15 lati; icosagono se ha 20 lati.
Proprietà dei poligoni
1. In ogni poligono ciascun lato è sempre minore della somma di tutti gli altri.
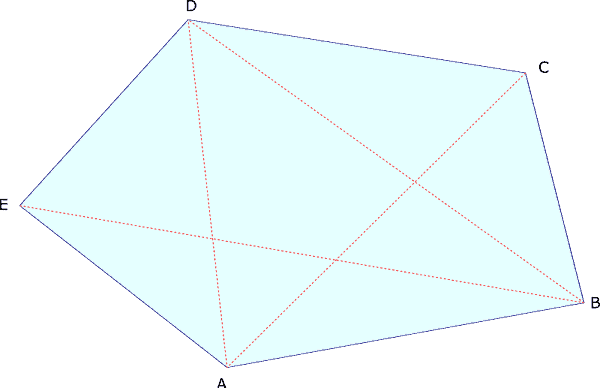
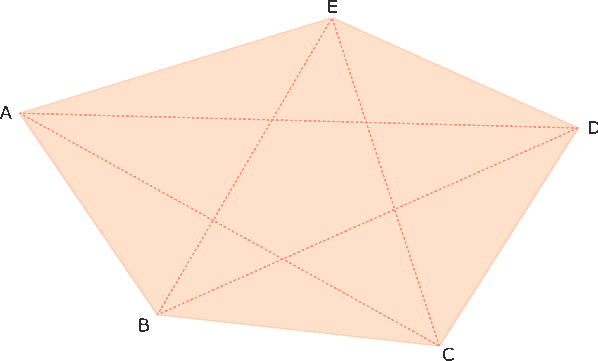
Disegniamo il pentagono ABCDE.
Abbiamo disegnato il pentagono ABCDE: cosa vedi?
Nel poligono disegnato ABCDE ciascun lato è minore della somma di tutti gli altri. Diciamo quindi che:
In ogni poligono ciascun lato è sempre minore della somma di tutti gli altri.
2. In un poligono di n lati per ogni vertice avremo (n – 3) diagonali.
Disegniamo il pentagono ABCDE.
Abbiamo disegnato il pentagono ABCDE.
Ora dal vertice A disegniamo tutte le diagonali possibili. Quante ne possiamo disegnare?
Riusciamo a disegnare solo due diagonali: AD e AC e questo vale per un qualsiasi altro vertice. Per esempio dal vertice B possiamo tracciare ancora due diagonali: BE e BD. Per ogni vertice abbiamo quindi (5 – 3) diagonali, cioè “il numero dei lati meno 3“.
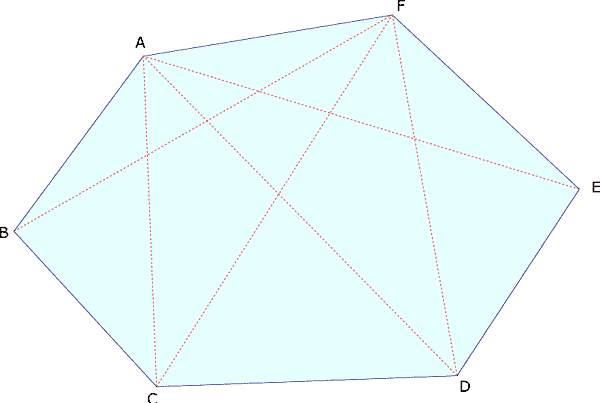
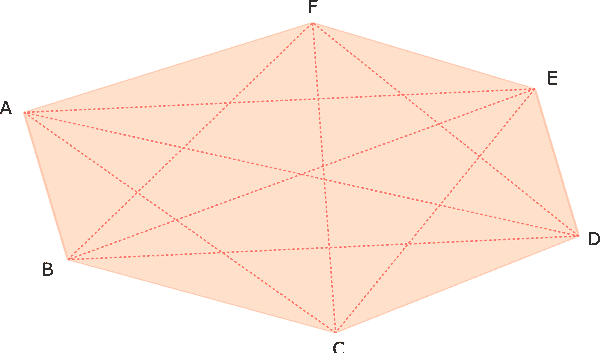
Il discorso vale per qualsiasi poligono. Per esempio nell’esagono ABCDEF per ogni vertice avremo 3 diagonali, cioè 6 – 3.
Possiamo quindi dire che:
In un poligono di n lati per ogni vertice avremo (n – 3) diagonali.
3. In un poligono di n lati il numero di diagonali è:
Prendiamo ad esempio alcuni poligoni e disegniamo tutte le diagonali possibili. Osserva.
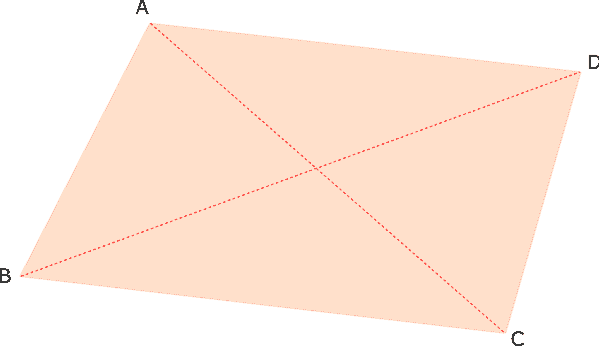
In un quadrilatero ne possiamo disegnare 2.
In un pentagono ne possiamo disegnare 5.
In un esagono ne possiamo disegnare 9.
Quindi, se osservi bene, possiamo disegnare:
4 · (4 – 3) : 2 = 2 nel quadrilatero
5 · (5 – 3) : 2 = 5 nel pentagno
6 · (6 – 3) : 2 = 9 nell’esagono.
Possiamo quindi dire che:
In un poligono di n lati in tutto il numero di diagonali è:
4. In un poligono qualsiasi la somma degli angoli esterni è sempre un angolo giro, cioè misura 360°, qualunque sia il numero dei lati.
Ciò lo si può verificare disegnando un poligono qualsiasi e tagliando tutti gli angoli esterni. Poi riuniamo tutti gli angoli esterni attorno a un unico vertice e in modo tale che risultino consecutivi a due a due. Che cosa osserviamo? Osserviamo che la loro somma è un angolo giro.
Quindi possiamo dire che:
In un poligono qualsiasi la somma degli angoli esterni è sempre un angolo giro, cioè misura 360°, qualunque sia il numero dei lati.